Understanding Option Delta

by Gavin in Blog

March 12, 2017 • 10 comments

Option delta is the most important greek for beginner traders to understand. This 2,000 word guide will tell you everything you need to know.

Contents

• What is Delta?
• Call Option Delta 
• Put Option Delta
• How Do I Calculate Option Delta?
• Delta And Gamma Relationship
• How Does Volatility Affect An Option Delta
• Delta Hedge Ratio
• What Are Common Delta Hedging Strategies?
• Delta And Probability

Delta is one of the four main option greeks, and any serious trader needs to have a thorough understanding of this greek if they hope to have any chance of success in the trading options. Read on if you want to learn about understanding options delta.

What is Delta?

Delta is the option’s sensitivity to changes in the underlying stock price. It measures the expected price change of the option given a $1 change in the underlying.

Call options have a delta between 0 and 1.

Put options have a delta between 0 and -1.

Call Option Delta

Assume a call option has a delta of 0.50, this indicates that for every $1 move in the underlying stock, the option price will change by $0.50.

If a call option has a delta of 0.20, the option price will change by $0.20 for every $1 move.

Using an example of XYZ stock trading at $50. A 6 month $50 call option is trading at $4.50 and has a delta of 0.50.

The next day, if XYZ rises to $51, the price of the option will have risen to $5.

Note that this example ignores any changes due to Vega, Gamma and Theta, the other main option greeks.

Using a live example from March 9^th, 2017 when AAPL was trading at $139.04.

The April 21^st $140 call option has a delta of 0.4667 and is trading at $2.62.

If AAPL rises $1 tomorrow, the price of the $140 call option will rise to $3.09. Again, this assumes no change in an other variable such as volatility and time to expiry.

Put Option Delta

Put options always have negative delta.

If XYZ is trading at $50 and a 6 month $50 put option is trading at $5 with a delta of -0.50, a 1$ move up in the stock will see the $50 put decline to $4.50.

Again using AAPL on March 9^th, 2017, the $140 put has a delta of -0.5354 and is trading at $3.40.

A $1 move up in AAPL will see the $140 put decline to $2.86.

How Do I Calculate Option Delta?

I can honestly say, I’ve never once calculated an options delta manually. There are so many tools out there these days that there really is no need to know how the Black Scholes model works.

By all means, dig in to it if you’re a bit of a math geek, but it’s not essential knowledge for successful option trading.

I have an excel calculator that you can download below if you like. Just plug in the underlying price, the strike price, risk free rate, implied volatility level, dividend yield and time to expiry and you will get the value of the option as well as all the greek values.

Download the Implied Volatility Calculator

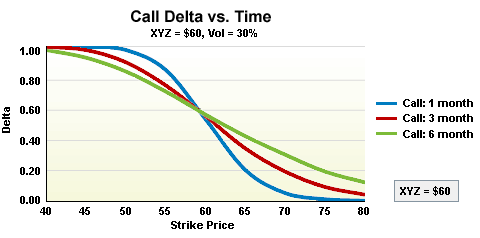
The 3 most important factors when calculating an options delta are the underlying price, the strike price and the time to expiry.

An important concept to understand is that as expiration approaches, the delta of out-of-the-money options will rapidly approach zero.

Less time to expiry, means less chance those out-of-the-money options will end up in the money. Therefore, they have a lower delta.

This is illustrated in the image below:

Delta And Gamma Relationship

I won’t delve into too much detail on gamma in this article, but it’s important to know that delta and gamma are closely related.

Gamma measures how much the delta will change given a $1 move in the underlying.

If delta is the “speed” at which option prices change, you can think of gamma as the “acceleration.”

You can learn more about gamma here.

An option with a gamma of +0.05 will see its delta increase by 0.05 for every $1 move in the underlying.

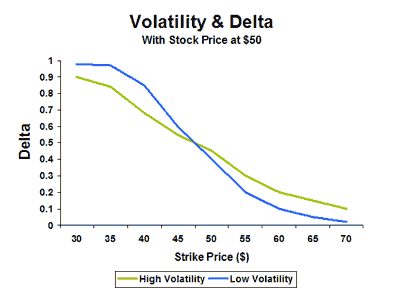
How Does Volatility Affect An Option Delta?

Option delta can change when implied volatility changes.

Changes in implied volatility will affect out-of-the-money and in-the-money options more than the at-the-money options.

If a stock is trading at $50 and has implied volatility of 15%, a 6 month $60 call option might have a delta of 0.07.

Volatility is low, so traders are not expecting big moves in the stock.

Now, assume implied volatility rises to 50%. Suddenly, traders ARE expecting a big move in the stock.

It is now much more likely that the $60 option will expire in-the-money and therefore it will have a higher delta than when implied volatility was 15%.

In this example the delta might have risen as high as 0.30. The call option will also now be much more expensive.

Option delta is a rough estimate of how likely an option is to expire in-the-money.

The image below shows the relationship between volatility and delta.

Sample Iron Condor Trading Plan

Delta Hedge Ratio

Delta hedging is an strategy that aims to reduce, or hedge, the price risk of an options trade.

Traders that own a long call option, have positive delta. They may choose to hedge some of this price risk by selling stock.

The delta of a position tells us the approximate directional exposure in terms of the stock.

This is sometimes referred to as Position Delta.

Taking our example of XYZ and a call option with delta of 0.50.

This is equivalent to owning 50 shares of the underlying stock, calculated as 0.50 delta x 100 shares per contract.

This makes sense, given that a $1 move higher in the underlying will see the call option gain $0.50.

This is the same return as if the trader owned 50 shares of the underlying.

Best of Options Trading IQ

If a trader owned 5 of these call options, they would have a total delta exposure of 5 contracts x 100 shares per contract x delta 0.50 = 250.

To completely hedge his price risk, the trader would sell short 250 shares, therefore cancelling out the delta exposure on the options.

However, remember that delta is a fluid number and this trade will not stay delta neutral for long (thanks to our old friend gamma).

Some delta neutral traders and market makers choose to hedge out their delta risk at the end of each day.

Others might choose to partially hedge their delta.

However, this can get expensive in terms of slippage and commissions.

Rather than selling short the stock, the trader could also use other options to hedge out the price risk.

For example, he might buy some long puts which would give him negative deltas.

Delta neutral traders want to keep delta as low as possible and maximize Theta.

What Are Common Delta Hedging Strategies?

Delta hedging strategies seek to reduce or eliminate directional risk from a position or portfolio.

The most common strategy is for a trader to buy or sell stock to offset the delta risk in an option trade.

Long stock has a delta of 1 and short stock has a delta of -1, so it is very easy to calculate how much stock you need to buy or sell to offset your option dalta.

At March 9^th, 2017 SPY was trading at 236.56 and the $240 April 21^st calls had a delta of 0.29.

Let’s assume a trader is short 1 contract. He has a delta position of -29.

In order to get delta neutral he would buy 29 shares.

You can see that the portfolio below is delta neutral but still has exposure to the other option greeks of gamma, vega and theta.

Neutralizing Delta Through Buying Shares

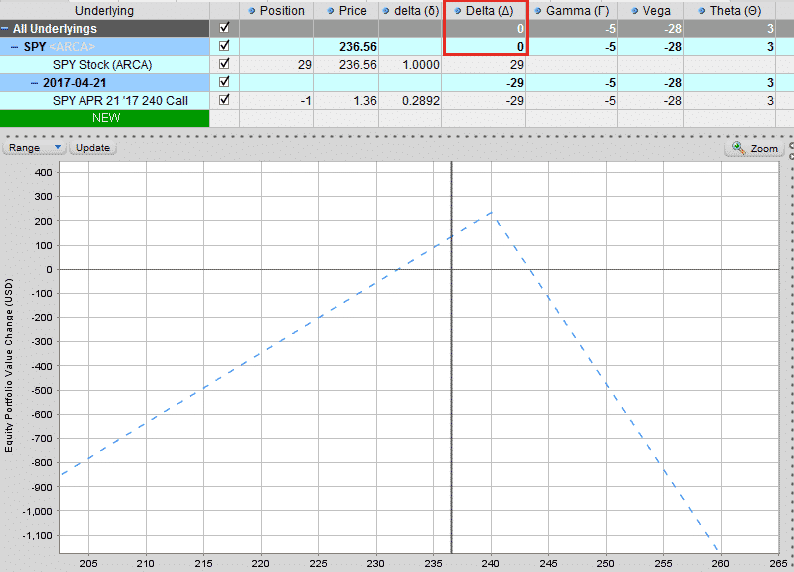
The position will not stay delta neutral for long. As SPY moves, the delta will change and if the trader wanted to stay delta neutral, he would need to buy or sell more stock.

If SPY rises, the call option delta will become more negative (makes sense as the trader wants the ETF to move back down away from his short call).

Therefore, to remain delta neutral the trader would need to buy more shares.

If SPY moves down, the trader would need to sell some of his shares to maintain a delta neutral position.

The trader adjusts the position back to delta neutral as often as his risk appetite demands.

Adjusting back to delta neutral will incur costs each time in terms of commissions and slippage.

Traders can also delta hedge a portfolio of options.

To do this they need to calculate the beta of each of the positions in the portfolio to come up with a portfolio level delta adjusted for beta.

They would then buy of sell the corresponding number of shares in SPY. I’ll provide more details on this soon.

Ultimate Guide To The Stock Repair Strategy

Delta And Probability

As a general rule, some traders use delta as the probability of an option expiring in-the-money.

For example, a call option with delta 0.20 has a roughly 20% chance of expiring in-the-money.

Now, unfortunately it’s not quite that simple, that’s why I said roughly 20% chance.

It’s not an exact science and there are many different variables that go into the options pricing model.

If all the variables (volatility, interest rate, dividends) remained constant over the course of the options life, then yes this probability would ring true.

However, these inputs are constantly changing.

Delta can be used as an estimate of probability and is certainly useful to know.

But, don’t assume that if you sell 20 delta puts you are going to win 80% of the time. It doesn’t work out that way in real life.

So be aware of the limitations of using delta as a probability.

Delta As An Estimate of Probability

While delta provides a decent estimate of the probability of and option expiring in-the-money, it also gives us a rough probability of our strike price getting touched at some point during its life (not just at expiry).

The formula is really very simple. If you have a 15 delta call, there is a roughly 15% chance of it expiring in-the-money and a roughly 30% chance of it being touched during the course of its life. You basically double the delta to get the chance of it being touched.

So, just because you are trading 15 delta iron condors, doesn’t mean that the strikes will only get touched 15% of the time, they will actually get touched 30% of the time.

If you think about it for a minute, it makes perfect sense. Take an at-the-money option with a delta of 0.50. The stock is right at the strike, so it has a 100% chance of touching that strike.

Keep this in mind next time you trade and use delta as an estimate of probability.

Please share this article on Facebook or Twitter if you think other traders will find it helpful.